Stroke's Theorem
Introduction :
This theorem states that the line integral of a vector field A around a closed curve is equal to the surface integral of the curl of A taken over the surface S surrounded by the closed curve.
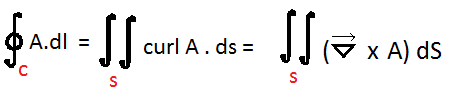
Proof :
consider a surface S enclsed in a vectorfieldA. as shown in figure the boundary of surface S is closed curve PQR.The line integral A around the curve PQR traced counter-clockwise is
Let the entire surface be divided into a large number of square loops. let the area enclosed by each infinite small loop be dS suppose 
be a unit positive outward normal upon dS. The vector area of the element is
We know that the curl of a vector field at any point is maximum line integral of the vector computed per unit area along the boundary of an infinitesimal area at that point. So the line integral of A around the boundary of the area dS is
this applies to all surface elements.Hence the sum of line integral of A around the boundaries of all the area element is given by
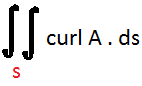
This is the surface integral of A.
The sum of the line integrals on the boundary line of curve is given by the above equatons Hence
This is Strokes Theorem.