General Procedure For Solving Poisson's Or Laplance's Equation
The Following procedure can be used in solving boundary value problem using Laplance's or Poision's equation:
1. If ƿv = 0
we use Laplance equation and if not (ƿv ≠ 0 ) we solve poisson's equation for a given problem.
Consider situations:
If V is only a function of one variable then direct integration will used and if V is a function of more variables the method used will be the method of sepration.
While using the above procedure the solution may not be unique but it contains a number of constants.
2. A numbers of boundries would be given and these boundary conditions are applied to obtian the values of the problems.
3. Substituting the value of constant in the solution, a unique solution of problem is obtained.
4. After obtaining the value of V, to find the value of E, D, J we use
(a) To find E :
![]()
(b) To find D :
use D = ϵ E
(c) To find J :
![]()
5. Find the charge Q if needed by using the
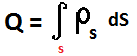
6. The capacity of two conductors can be found using
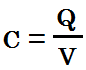
7. The resistance of an object can be found using
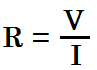
Where
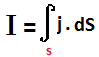
This is all about General Procedure For Solving Poisson's Or Laplance's Equation .


